カーボンナノチューブの高分解能光電子分光
カーボンナノチューブ
カーボンナノチューブは、炭素(カーボン)だけからなる、半径1ナノメートル(1ナノメートル、1nm=1mmの百万分の1の長さ)程度、長さ1ミクロン(1μm=1mmの千分の1の長さ)程度の細長い筒状の物質です。図1にカーボンナノチューブの模式的な構造と電子顕微鏡写真を示します。カーボンナノチューブは、1991年に飯島澄男氏らによって発見された新しい物質であり、基礎、応用の両面からたいへん興味深い性質をもっています。

図1 カーボンナノチューブの模式的な構造(a)と電子顕微鏡写真(b)
たとえばカーボンナノチューブは機械的な強度が強く、軽量なため補強材として使うことができます。またカーボンナノチューブは細長い構造をしているので、原子間力顕微鏡や走査トンネル顕微鏡の探針として用いることにより、これまで観測が困難であったDNAやタンパク質なども直接見ることができます。またカーボンナノチューブの先端部分を電子銃とした薄型ディスプレイや単電子トランジスターなどのナノ電子デバイスへの応用も期待されています。
風変わりな一次元金属状態
基礎研究の観点からは、カーボンナノチューブは金属と半導体の中間に位置する「半金属」であり、1次元的な構造に由来して様々な興味深い性質を持っています。1950年に朝永振一郎氏は、仮想的に大きさの無視できる細長い糸状の1次元金属を初めて理論的にとりあげ、その変わったふるまいを考察しました。その後、ラッティンジャーにより、理論研究がさらに進められましたので、1次元金属の電子状態は「朝永ーラッティンジャー液体」と呼ばれています。一方、通常の3次元的な広がりを持つ金属(3次元金属)の電子状態は「フェルミ液体」と呼ばれます。
1次元金属では、電子が動ける方向が一方向に制限されているため、量子力学的なゆらぎがたいへん大きく、3次元金属とは全く異なる性質をもつことが理論的に予測されました。
たとえば3次元金属の場合、エネルギーが最も低い電子軌道から、最大のエネルギー(フェルミエネルギーと呼び、ここではエネルギーの原点にとります)を持つ電子軌道まで、電子が1個づつ配置されています。一方、一次元金属の場合は、フェルミエネルギーに近づくにつれて、占有している電子数の割合(ρ)が次第に減少します。具体的にはエネルギーωの関数として、
ρ= A |ω|α (Aは定数)
のように表されます。すなわち、フェルミエネルギーに近づくにつれてρがベキ乗則にしたがって減少することを示してます。3次元金属の場合、フェルミエネルギーに近づいても占有している電子の割合がほぼ一定です。一方、フェルミエネルギーを持つ電子の個数に着目し、低温から高温に温度をあげていくと、やはり温度Tの指数関数として、
ρ= BT α (Bは定数)
のようにベキ乗則で表されます。αの値は、理想的な1次元金属の場合には、精密な計算がなされており、実験と理論とを精密に比較することにより、朝永ーラッティンジャー液体状態が実現しているかどうかを確めることができます。
カーボンナノチューブの光電子分光実験
光電子分光実験は、測定したい物質に紫外線、X線を照射し、飛び出してくる電子(光電子と呼びます)のエネルギーや運動量を分析して、物質の中における電子のふるまいを直接的に調べることができます。これまでにもカーボンナノチューブについて光電子分光実験は行われてきましたが、朝永ーラッティンジャー液体が実現していることを示す実験結果は得られませんでした。その主な理由は、測定試料の大きさがまちまちで、不純物を多く含んでおり、また光電子分光測定の精度が十分高くなかったことがあげられます。
この研究では、HiSORの高強度、高分解能のアンジュレーター放射光と、高分解能光電子エネルギー分析器とを組み合わせることにより、フェルミ準位ごく近傍でみられる電子の振る舞いを精密に決定することをめざしました(図2参照)。
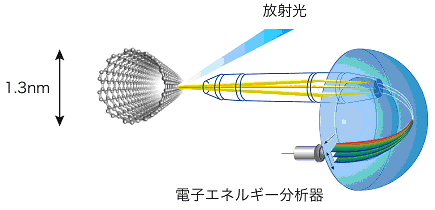
図2 高分解能光電子分光実験の模式図。放射光をカーボンナノチューブに照射して、放出される光電子のエネルギーを精密に分析します。
この目的のためには、測定するカーボンナノチューブの直径がそろっている必要があり、不純物が含まれていないことが重要です。また試料の中に含まれている水分を超高真空槽の中で加熱処理により除去する必要があります。こうした課題を一つづつ解決することにより、はじめてカーボンナノチューブの本質的な電子状態を観測することができるようになりました。
図3に励起光のエネルギーを30eV(波長41nm)にして得られた結果を示します。横軸は、電子が原子核にどのくらい強く束縛されているかをあらわす「結合エネルギー」で、縦軸は電子の数を表します。このようなグラフのことを「光電子スペクトル」と呼びます。測定温度は絶対温度310K(摂氏37℃)から10K(-263℃)まで変化させました。
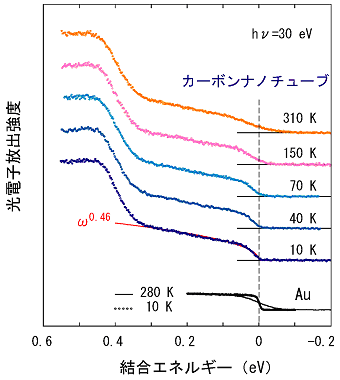
図3 カーボンナノチューブの高分解能光電子スペクトル
結合エネルギーがゼロ(0eV)のところ(=フェルミエネルギー)に存在している電子は、原子核のある場所に束縛されずに固体内部を自由に動き回ることができます。すなわち結合エネルギーがゼロのところに電子が存在することが「金属」であることの必要条件です。図3で分かるように310Kでは、たしかに結合エネルギーがゼロのところに強度がありますが、温度を下げて10Kになるとほとんど強度が無くなっていることがわかります。
一方、3次元金属の典型物質として金(Au)の光電子スペクトルを見ると10 Kでも明瞭に結合エネルギーがゼロのところに電子が存在していることが分かります。低温でもカーボンナノチューブは金属なので、これは金とは著しく異なる性質をもつことが見ただけでも分かります。
結合エネルギーが0.2eVから0eVの範囲でカーボンナノチューブの光電子スペクトルの形状を見てみましょう。結合エネルギーが減少するにつれて放出される電子の強度がベキ乗にしたがって減少していく様子が分かります。これはすでに述べたρ=A |ω|αという関数で大変よく記述され、αの値は0.46±0.10と求めることができました。
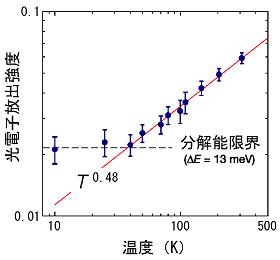
図4 結合エネルギーがゼロのところの電子の数の温度依存性
次に結合エネルギーがゼロのところの光電子放出強度に注目して、温度の関数として求めたのが図4です。横軸と縦軸を対数にとると40K以上で直線的になることがわかります。このふるまいは、既に述べたρ=BT αの式でよく表されます。この式を用いて求めたαの値は0.48±0.08となりました。二つの異なる方法で求めたαの値は実験誤差の範囲でよく一致しました。
理論的にはα=0.46と計算されていますので、実験で得られたαの値と高い精度で一致することが分かりました。このことはカーボンナノチューブにおいて朝永ーラッティンジャー液体状態が実現している明確な証拠となります。この実験により世界ではじめて1次元金属の電子状態が朝永ーラッティンジャー液体状態にあることを直接的に示すことができました。すなわちこれまでは仮想的なモデルにすぎないと思われていた朝永理論が約半世紀を経て、見事に検証されたということになります。
この研究成果は、ネイチャー誌2003年12月4日号に掲載され、朝日新聞、産経新聞などでも報道されました。これに続く研究として、HiSORでは、カーボンナノチューブの中に、炭素だけからなる球状の物質(フラーレン)が入ったピーポッドの電子状態を精密に決定し、その研究成果を2006年にPhysical Review B 73 (2006) 075406で公表しました。











