強磁性ニッケルの高分解能光電子分光
強磁性金属ニッケル
ニッケル(Ni)は周期律表で28番目の元素であり、鉄やコバルトと並んで、代表的な電気を通す磁石です。ニッケルが磁石になるうえで、電気伝導を担っている電子の「スピン」が重要な役割をはたします。「スピン」というのは、電子の自転と対応づけられ、右回りと左回りに回転する電子をそれぞれ「上向きスピン」および「下向きスピン」と呼びます(図1)。電子はそれ自体が小さな磁石になっていると考えられます。ニッケルが磁石になるのは、全体として、上向きスピンと下向きスピンの数が異なっており、またスピンが平行に配列(「強磁性」と呼ばれます)していることに由来します(図1)。金属が強磁性になるメカニズムは、いまだに完全な理解にはいたっておらず、最先端の理論研究が進められているところです。
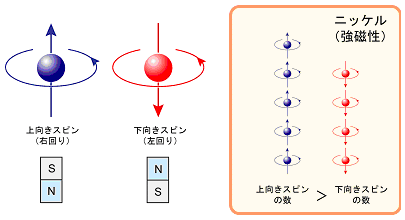
図1 電子のスピン
ニッケルは、ステンレス鋼、めっき、変圧器の鉄心、磁気ヘッドなど産業においてきわめて重要な金属ですが、比較的産出量が少なく戦略的にも重要な「希少金属」の中の一つにあげられています。周期律表でニッケルの下の元素にパラジウム(Pd)と白金(Pt)があります。これらはいずれも触媒として大変重要な物質であり、希少金属です。物質の性質(物性といいます)は、結晶構造および電子状態が支配します。ニッケルとパラジウムは、結晶構造も電子状態もよく似ているにも関わらず、ニッケルは磁石になり、パラジウムは磁石になりません。こうした違いがどこにあるのか、ということは固体中で電子が運動するときに、どのような相互作用を受けるか、ということと密接に関わっています。
多体相互作用
固体中の電子は、いろいろな相互作用を受けます。代表的なものとしては次の3つの相互作用があげられます(図2参照)。
(1)電子ー不純物相互作用
固体中に含まれる不純物や格子欠陥との相互作用。低温での電気抵抗率や磁気的性質に重要な役割を果たします。
(2)電子ー格子相互作用
結晶を構成している格子振動との相互作用。金属の電気抵抗率の温度依存性に寄与します。低温でアルミニウムや鉛が超伝導となるための重要な相互作用です。
(3)電子ー電子相互作用
電子はマイナスの電気を帯びているので、互いに電気的に反発する相互作用。これは物質が磁石になるために重要な相互作用です。また酸化物高温超伝導体が高い臨界温度を持つ理由も電子同士の強い反発に由来すると考えられています。
これらをまとめて「多体相互作用」と呼びます。固体中には多数の電子があり、それぞれこうした多体相互作用を受けながら運動しています。固体が磁石や超伝導になるかどうかということは電子に働く多体相互作用と密接に関係しています。すなわち多体相互作用が複雑で多彩な固体の性質を生み出しているのです。したがって固体の性質を考えるうえで、電子がどのような多体相互作用をどのくらいの強度で受けているのかを実験的に解明することは大変重要となります。
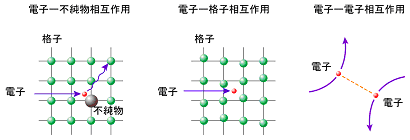
図2 固体の中の電子が受ける様々な多体相互作用
高分解能角度分解光電子分光実験
光電子分光実験は、測定したい物質に紫外線、X線を照射し、飛び出してくる電子(「光電子」と呼びます)のエネルギーや運動量を分析して、物質中の電子のふるまいを直接的に調べる手法です。これまでニッケルの光電子分光実験は精力的に行なわれてきましたが、どのような多体相互作用がどのくらいの強さで働くのか、ということに関しては、ほとんど分かっていませんでした。
この研究では、HiSORの高強度・高分解能のアンジュレーター放射光と、高分解能光電子エネルギー分析器とを組み合わせることにより、電子に働く多体相互作用を精密に測定することをめざしました。ここでは角度分解光電子分光という手法を用いて固体中の電子の「運動量」(質量と速度のかけ算であらわされます)とエネルギーの関係をしらべました。
固体内部で、最もエネルギーが高い(これを「フェルミエネルギー」と呼び、ここではμと書きます)電子は、原子核のある場所に束縛されずに固体内部を自由に動き回ることができます。これは「自由電子」とよばれます。自由電子がどの方向にどのくらいの速度で運動しているのか(ここでは運動量で考えます)を曲面で表したものを「フェルミ面」と呼びます。強磁性ニッケルでは、理論計算(バンド計算)により、図3に示すようなフェルミ面が計算されています。
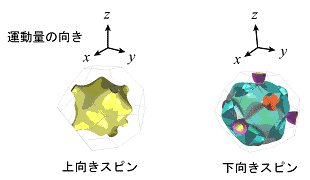
図3 ニッケルのフェルミ面(理論計算)[1]
図4に角度分解光電子分光実験により測定したフェルミ面の切断面を示します。色の濃い部分が光電子放出強度が高いところで、実測されたフェルミ面を示します。私たちは本研究によりニッケルのフェルミ面を高精度に決定することができました。得られた結果を最新のバンド計算と比較してみます。図4で赤の破線および青の実線は、それぞれ理論的に計算された上向きスピン、および下向きスピンのフェルミ面の断面です。観測されたフェルミ面の形状は、理論的によく説明できることが明らかになりました。
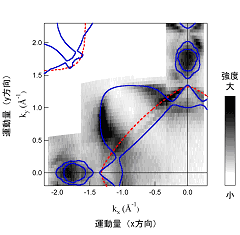
図4 ニッケルのフェルミ面の断面の実測値および理論値
次にこのフェルミ面の対称性の高い場所をとって、電子のエネルギーと運動量の関係(「分散関係」といいます)を精密に調べてみました。これによって、多体相互作用がどのように働いているのかを詳細に調べることができます。ここではエネルギーの原点をフェルミエネルギーを基準にとります。一般に、固体中の電子の分散関係はたいへん複雑ですが、フェルミエネルギーにごく近いところでは、電子のエネルギーE と運動量p との関係は次のような簡単な二次関数でよく近似式され、グラフでは図5のような放物線となります。
p2
E = ――― - μ
2m*
ここでm* は電子の「有効質量」と呼ばれ、固体中の電子の動きやすさを示します。有効質量が重いと電子は動きにくく、軽いと電子は動きやすいことになります。放物線の形とm* の関係を図5の右側に示します。フェルミエネルギーに近いところでは、m* が大きいほど、傾きがゆるやかになります。多体相互作用が働くと有効質量が大きくなりますので、分散関係の傾きの変化を精密に調べることにより、相互作用の強度やその由来を実験的に決定できます。
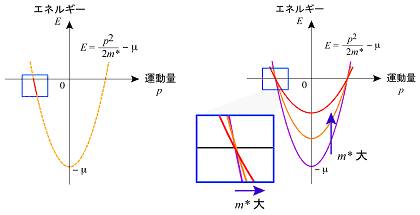
図5 固体中の電子の運動量とエネルギーの近似式
図6に励起光のエネルギーを21.2eV(波長58.5nm)〜35.0eV(波長35.4nm)まで変化させて、フェルミ面のある場所を角度分解光電子分光で調べた結果を示します。横軸は運動量、縦軸はエネルギーです。測定温度は絶対温度10K(-263℃)に設定しました。青い丸は、強度が極大となる場所の分布を示しています。フェルミエネルギーにごく近いため、放物線が拡大されて直線的に見えます(図5参照)。実験では、上で述べたように固体中の電子がもつ最大のエネルギーがフェルミエネルギー(エネルギー=0meV)なので、フェルミエネルギーよりも高いエネルギーに電子は存在しません。これまでの研究から図6の左側の分散関係は上向きスピン、右側の分散関係は下向きスピンに由来しています。とりわけ29.0eVで励起した場合には、対称性からΣ1バンドと呼ばれます。
図6の分散関係をよく見ると、上向きスピン電子の分散関係は、ほぼ直線的ですが、下向きスピン電子の分散関係は、約-40meVから0meVに向かって、ほんのわずかに折れ曲がっているのがわかります。これは、放射光のエネルギーを変えても同じふるまいです。この折れ曲がりは、多体相互作用を受けて、下向きスピンの分散関係が変化していることを示します。図5で有効質量m* が大きくなると、フェルミエネルギーのところで分散関係の傾きがゆるやかになることが分かります。傾きがゆるやかになる方向に変化するほど、すなわち折れ曲がりの度合いが大きくなればなるほど、強く相互作用を受けていることが分かります。
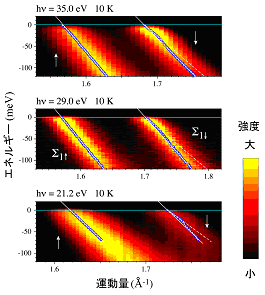
図6 ニッケルの実験で観測された分散関係
図7に21.2eVで別のフェルミ面を調べた結果を示します。この分散関係は、下向きスピン電子に由来するもので、対称性からΣ2バンドと呼ばれます。同じ下向きスピンでもΣ2バンドの方がΣ1バンドに比較して大きく折れ曲がりが生じているのが分かります。すなわち同じ下向きスピンであってもフェルミ面が異なると多体相互作用の強度が異なっていることが初めて明らかになりました。
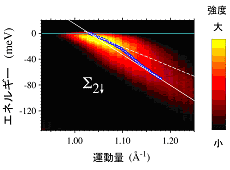
図7 ニッケルの実験で観測された分散関係
分散関係を直線で近似し、直線からのずれを描いたのが図8です(これは「自己エネルギーの実部」となります)。上向きスピンの方はエネルギーによらずほぼゼロですが、下向きスピンの方は約-25meVで最大値をとった後で0meVに向かって減少します。このふるまいは電子ー格子相互作用を考慮した理論計算を行うと、実験を良く説明できることが分かりました(図8の緑の実線)。すなわち下向きスピン電子は電子ー格子相互作用によって有効質量が重くなっていたのです。また電子ー格子相互作用の強さは、電子スピンの向きやフェルミ面によって異なることが初めて明らかになりました。より詳しい解析によりΣ1バンドの電子ー電子相互作用に関しては、上向きスピンの方が下向きスピンよりも強く働いていることも明らかになりました。
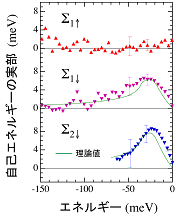
図8 実験的に求めた自己エネルギーの実部
放射光を用いた高分解能角度分解光電子分光実験により、ニッケルの電気伝導、強磁性などの物性と密接に関わる多体相互作用を初めて精密に評価することができるようになりました。この手法をさらに展開することにより、ニッケルと結晶構造や電子構造が似ているのにパラジウムや白金の物性がなぜ異なるのかという問題についても明らかできると期待できます。本研究手法は、強磁性や触媒など機能性の高い材料開発や希少金属の代替物質の基礎研究にも貢献できると考えています。
この研究成果は、Physical Review B 72 (2005) 214438で公表されました。
[1] http://www.phys.ufl.edu/fermisurface/











