低エネルギー放射光によるノード準粒子状態の解明
概要
d波の超伝導状態では、低エネルギー準粒子が超伝導ギャップのノード点にのみ生き残っている。このノード準粒子が低エネルギー物性を支配しており、その振る舞いが興味を集めている。しかし、銅酸化物高温超伝導体では、CuO2二重層によってノード準粒子状態が2つに分裂しており、輸送係数などのマクロ物性測定では、平均的な情報しか得られない。また、これまでの角度分解光電子分光研究では、実験分解能などの問題から、2種類のノード準粒子の性質を分解するのが非常に難しく、結果についても意見が分かれていた。今回の成果は、HiSORの低エネルギー放射光を活用することで、ノード方向の微小な分裂を分解し、ノード準粒子の本来の散乱確率を、直接観測により明らかにしたものである。これにより、ノード準粒子の散乱確率が、特異な温度・エネルギー依存性を示すこと、結合・反結合バンドの散乱確率の違いが、超伝導状態における散乱過程について、大きな手掛かりとなっていることを明らかにした。
背景
銅酸化物系の高温超伝導体が、通常の超伝導体と決定的に違う点は、超伝導ギャップに強い異方性があり、超伝導状態でもギャップの開かないノード点が存在することだ。ノード点の準粒子が、超伝導状態における熱力学特性や輸送係数などの低エネルギー物性を支配している。超伝導状態で点状に生き残っているノード準粒子が、通常のフェルミ流体の準粒子と同様に振る舞うのか、特異的な挙動をしめすのか、長いこと興味の対象となっていた。しかし、超伝導状態におけるノード準粒子の散乱確率を測定するのは簡単ではない。例えば直流の電気抵抗は消滅する。これまでは、マイクロ波や光学などの交流伝導度の研究が行われてきたが、その解釈が一意的でなく問題となっていた。特に、超伝導転移温度の高い銅酸化物は図1(a)に示すように二重のCuO2面を有しており、面間の混成によって、図1(b)に示すように、状態が結合バンドと反結合バンドに分裂している。マクロ物性測定では、両バンドについての平均的な情報しか得られない。
それに対して、角度分解光電子分光は、ひとつの準粒子励起をエネルギー・運動量空間で分解して直接観測できる強力な手法である。スペクトルのピーク位置とピーク幅から、準粒子の分散と散乱確率を同時に決定できる。しかし、図1(b)に示すように、ノード方向では結合バンドと反結合バンドが極めて近接しており、従来の実験では有限の分解能のために、両バンドの準粒子の性質を分解することが困難であった。
本研究では、HiSORの低エネルギー放射光 (hν= 7.57 eV) を用いて、結合・反結合バンドについて分解したノード準粒子散乱確率を直接観測した。高い運動量分解能と、放射光のエネルギー可変性を活用することで、結合・反結合バンドに分裂したノード方向のスペクトル関数の鮮明な像を得た。散乱確率の詳細なエネルギー・温度依存性より、低エネルギー準粒子が、弾性散乱の影響を強く受けていることを明らかにした。そして、結合・反結合バンドの散乱確率の違いが、主要な散乱源がCuO2二重層の外側にあることを示していることを明らかにした。
角度分解光電子分光実験において、低エネルギー放射光を用いることは、多くの利点がある。まず、図2に示すように、低エネルギー領域では光電子放出角が大きくなるために、運動量空間がより広い角度領域に拡大されて観測されることになる。つまり、装置の角度分解能が同じでも、準粒子の運動量分解能が大きく向上する。次に、低エネルギー領域では、光電子の脱出深度が増大するために、表面の劣化や表面状態などの影響を最小限に抑えることができる。一方で、光電子の平均自由行程が長くなることは、光電子遷移の終状態のエネルギー不確定性が抑制され、終状態による選択則が厳しくなることを意味する。従って、低エネルギー励起の角度分解光電子分光では、放射光によるエネルギー可変性が決定的に重要であり、実際、我々は、光電子スペクトルが励起光エネルギーに激しく依存することを見出した。本研究では、結合バンドと反結合バンドが同時にはっきりと観測されるように、放射光のエネルギーを調節してから実験を行い、これらの準粒子の性質を分解することに成功した。
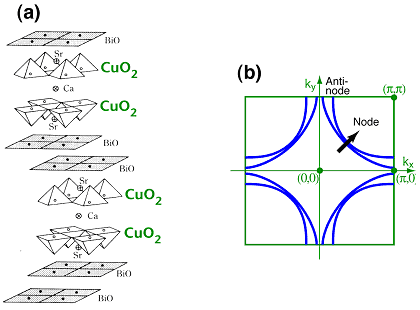
図1 (a)銅酸化物高温超伝導体 Bi2Sr2CaCu2O8+δの結晶構造。二重のCuO2面をもつ。(b) Bi2Sr2CaCu2O8+δのフェルミ面の概略図。矢印は、本研究で対象としたノード方向。
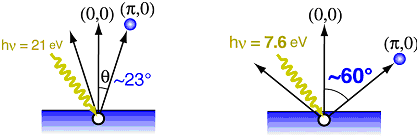
図2 励起光のエネルギーによる光電子放出角の違い。左:通常のエネルギー hν= 21 eVの励起光を用いた実験の場合。右:hν=7.6 eVの低エネルギー放射光を用いた実験の場合。
研究内容
実験は、広島大学放射光科学センターの HiSOR BL9にて行った。高分解能角度分解光電子分光実験に関して、低エネルギー放射光が得られるな光源は、他には見られない。試料は、ほぼ最適ドープ (Tc = 86 K) のBi2Sr2CaCu2O8+δ単結晶を用いた。図3、4に、hν= 7.57 eVの低エネルギー放射光で測定した光電子スペクトルを示す。温度は9 Kの超伝導状態、向きは図1(b)に示す超伝導ギャップのノードの方向で測定した。図3を見ると、約70meV における準粒子の繰り込み構造が、従来の実験に比べ極めて明瞭に観測されていることがわかる。さらにフェルミ準位近傍では、図4に示すように、CuO2二重層による結合バンドと反結合バンドのわずかな分裂 (kA-kB = 0.0075Ǻ-1) がはっきりと分解されており、従来の実験に比べて格段に高い運動量分解能が達成されていることがわかる。ノード準粒子のピーク幅はΔk = 0.0065Ǻ-1で、これは150Ǻ以上の緩和距離に相当する。
まず、広範囲における準粒子のエネルギー・温度依存性を得るために、二重層分裂のパラメーターを固定して、運動量分布曲線のフィッティング解析を行った。分散の直線からのずれより決定した準粒子繰込エネルギーを図5(a)に、ピークの運動量幅から直接決定した準粒子の散乱確率を図5(b)に示す。それぞれ、自己エネルギーの実部と虚部に対応する。70meV付近をみると、実部のピーク構造と虚部の段差構造が良く対応していることがわかる。自己エネルギー実部のKramers-Krönig変換が自己エネルギー虚部と良く一致したことから、実験精度の高さが示された。超伝導転移温度の上下に渡って測定したノード準粒子散乱確率の温度依存性を、図5(c)に示す。超伝導転移とともに、散乱確率の大部分 (60-70 %) が抑制されることを明らかにした。この散乱確率の段差の大きさは、非弾性散乱の効果だけで理解することは難しく、d波超伝導ギャップが開くことによって弾性散乱も抑制されることを示している。
低温、低エネルギー領域については、結合・反結合バンドの分解が可能である。2つの独立なピークを仮定して運動量分布曲線をフィ ッティング解析し、結合・反結合バンドの散乱確率を分解した結果を図5(c)に示す。フェルミ準位上では、両者の散乱確率はほぼ同じであるが、エネルギーとともに反結合バンドの散乱確率が結合バンドの散乱確率を上回っていることがわかる。興味深いのは、図5(b)、図5(d)のどちらの解析結果でも、低エネルギー領域 (|ω|<40 meV)の散乱確率が極めて直線的なエネルギー依存性を示すことだ。通常のフェルミ流体では、散乱確率はエネルギーの自乗以上の冪 ∝ωn (n≥2) に従う。この特異な現象は、d 波超伝導ギャップによってノード近傍に線形の状態密度∝|ω|が形成されていることを反映して、弾性散乱確率がエネルギー依存性を示しているものと考えられる。光電子分光で観測される1粒子散乱確率が線形のエネルギー依存性を示すこと、それに比べて輸送係数として観測される散乱確率が小さくなっていることは、低エネルギー準粒子が微小角前方弾性散乱の影響を強く受けていると理解される。このとき、散乱の性格は準粒子と散乱源の距離に依存している。結合バンドより反結合バンドの準粒子がより強く散乱されていることから、結合・反結合状態の位置分布の違いを考えると、主要な散乱源はCuO2二重層の外側にあること、すなはちドーピングによって導入されたCuO2面外の不規則性が高温超伝導状態に深刻な影響を与えていることが示唆される。
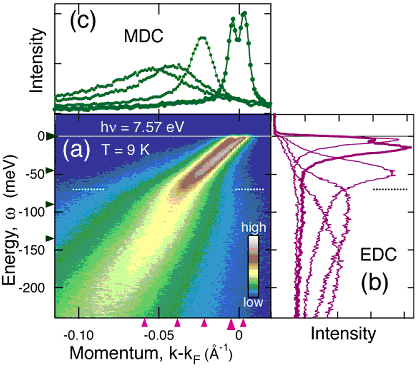
図3 低エネルギー放射光 (hν= 7.57 eV) を用いて得たノード方向の光電子スペクトル。 (a) エネルギー・運動量空間における、光電子強度表示。(b)エネルギー分布関数。(c)運動量分布関数。
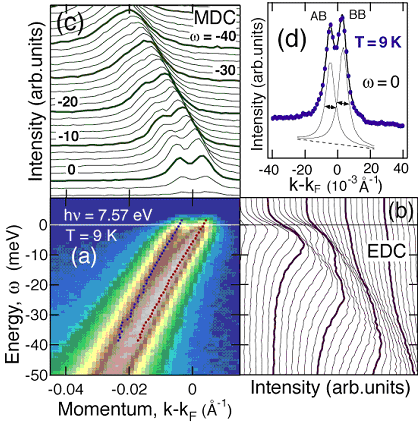
図4 ノード方向の光電子スペクトルのフェルミ準位近傍の拡大図。(a)エネルギー-運動量空間における光電子強度表示。(b) エネルギー分布関数。(c)運動量分布関数。(d) フェルミ準位における運動量分布関数。観測されたノード準粒子のピーク幅はΔk = 0.0065Å-1。
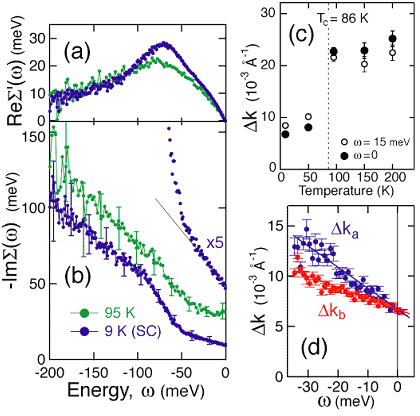
図5 (a)ノード準粒子の繰込エネルギー ReΣ(ω)。分散の直線からのずれより決定した。(b)ノード準粒子の散乱確率-ImΣ(ω)。ピークの運動量幅より直接決定した。 (c)ノード準粒子の散乱確率の温度依存性。(d)結合バンドΔkB、反結合バンドΔkAについて分解した準粒子散乱確率のエネルギー依存性。
本研究の意義
従来、準粒子の性質を測定する主な手法は、光学伝導度、マイクロ波伝導度、熱伝導率などのマクロな輸送係数の測定であった。これらの低エネルギー実験では高いエネルギー分解能が得られる。しかし、マクロ物性測定では、個々の準粒子の性質を複雑に重ね合わせた情報しか得られず、測定データを解釈するために仮想的なモデルを設定する必要があった。一方、角度分解光電子分光は、1つの準粒子励起を直接観測できる強力な手法だが、実験分解能が準粒子の測定精度に直結するため、今までは準粒子の性質を詳細に決定するのが難しかった。本研究の取り組みによって、従来より格段に高い分解能で準粒子の観測が可能になり、エネルギー・運動量空間で分解した準粒子の性質を、マクロ物性と直接比較できるようになった。この新しい手法は、固体中の電子に作用する多体効果を解明するのに決定的な役割を果たすことが期待される。
原著論文は、Yamasaki et al., Phys. Rev. B 75, 14503 (2007).











